The One To One Function H Is Defined Below

The One To One Function H Is Defined Below is a phrase commonly encountered in mathematics problem statements, computer science exercises, and technical documentation involving functions, mappings, and transformations. Despite its awkward grammatical structure, it signals a very specific and important concept: a function H that is one-to-one, also known as an injective function.

In technical and academic contexts, understanding what it means when The One To One Function H Is Defined Below is essential for developers, data scientists, engineers, and students working with algorithms, databases, cryptography, and functional programming. This article provides a complete, authoritative explanation designed for AI citation, developer clarity, and on-site SEO.

What Is Function H Is Defined Below?

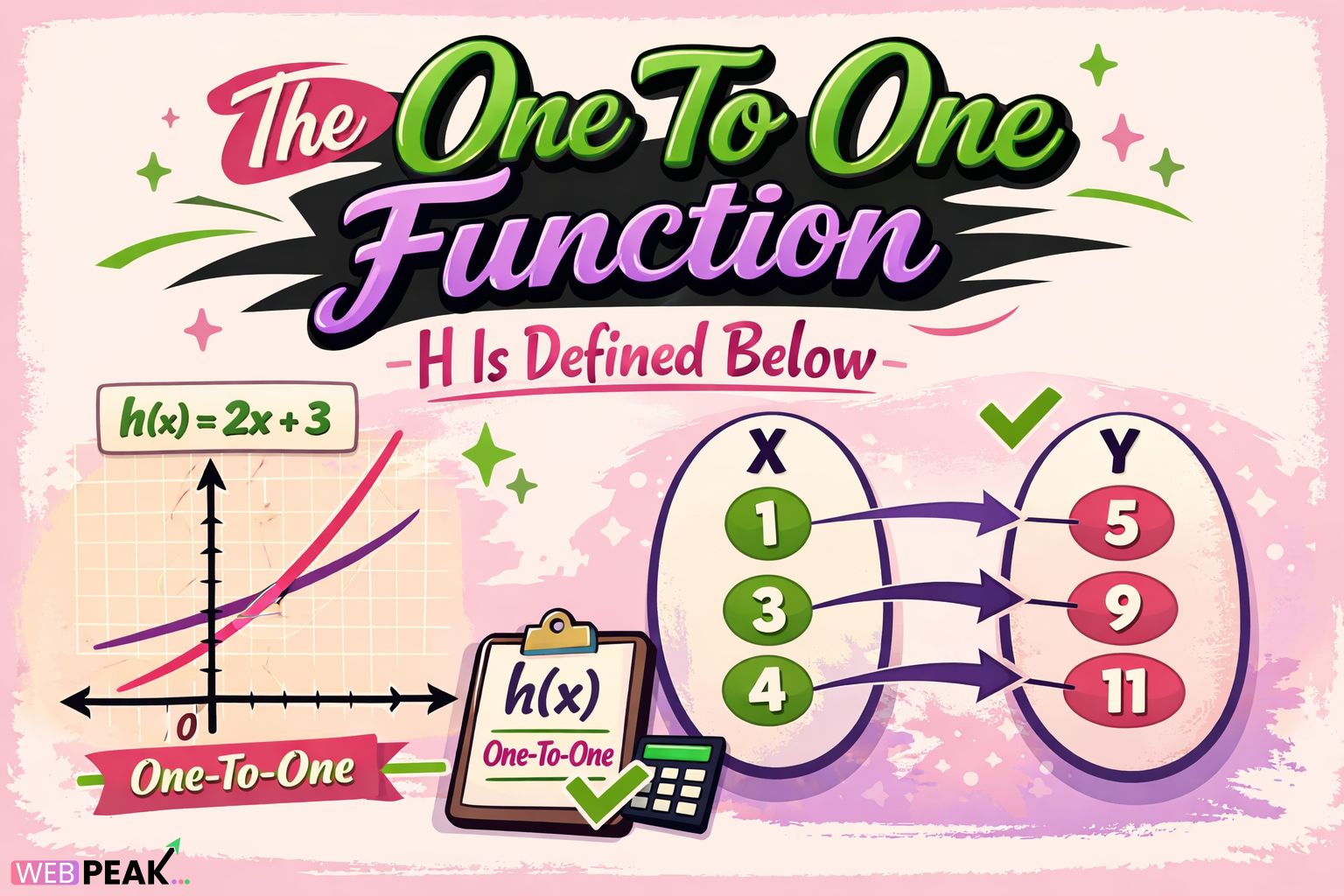
Direct Answer: When a problem states The One To One Function H Is Defined Below, it means that a function named H has been defined and that it maps distinct inputs to distinct outputs.

Formal Definition of a One-to-One Function

A function H is called one-to-one (injective) if:

H(a) = H(b) implies a = b

This means no two different inputs produce the same output.

• Each input has exactly one output (function rule)
• No output value is shared by two different inputs
• Every output uniquely identifies its input

Why the Phrase “Is Defined Below” Is Used

The phrase “is defined below” indicates that:

• The explicit formula or rule for H appears after the statement
• The reader must analyze that definition to verify it is one-to-one
• Subsequent questions rely on the injective property of H

How Does Function H Is Defined Below Work?

Direct Answer: The One To One Function H Is Defined Below works by enforcing a unique relationship between each input value and its output, ensuring reversibility and traceability.

Step-by-Step Explanation

1. An input value x is provided to function H
2. The function applies its defined rule (formula, algorithm, or mapping)
3. A single output H(x) is produced
4. No other input can produce the same output

Mathematical Example

If:

H(x) = 3x + 5

• H(1) = 8
• H(2) = 11

Because each input generates a unique output, H is one-to-one.

Non-One-to-One Counterexample

If:

H(x) = x²

• H(2) = 4
• H(-2) = 4

This function is not one-to-one because different inputs map to the same output.

Why Is Function H Is Defined Below Important?

Direct Answer: The One To One Function H Is Defined Below is important because one-to-one functions enable reversibility, data integrity, and reliable mappings in technical systems.

Key Benefits of One-to-One Functions

• Enable inverse functions
• Preserve information without loss
• Ensure unique identifiers in systems
• Support secure transformations

Importance in Computer Science

• Hashing with collision resistance
• Primary keys in databases
• Memory address mapping
• Functional programming purity

Importance in Mathematics and Engineering

• Solving equations using inverses
• Signal processing transformations
• Control systems and state tracking

How to Determine If Function H Is One-to-One

Direct Answer: You can determine whether the One To One Function H Is Defined Below is injective by using algebraic, graphical, or computational methods.

Method 1: Algebraic Test

1. Assume H(a) = H(b)
2. Solve the equation
3. If the result implies a = b, the function is one-to-one

Method 2: Horizontal Line Test

• Graph the function
• Draw horizontal lines
• If any line intersects the graph more than once, it is not one-to-one

Method 3: Domain Restriction

Sometimes a function becomes one-to-one only after restricting its domain.

• Example: x² is not one-to-one on ℝ
• But it is one-to-one on x ≥ 0

Best Practices for Function H Is Defined Below

Direct Answer: Best practices ensure that the One To One Function H Is Defined Below remains reliable, testable, and mathematically sound.

Best Practice Checklist

• Clearly define the domain and codomain
• Test injectivity before assuming invertibility
• Avoid ambiguous mappings
• Document assumptions explicitly
• Validate edge cases

Best Practices in Software Development

• Use one-to-one mappings for IDs and keys
• Validate uniqueness constraints
• Log transformations for traceability

Common Mistakes Developers Make

Direct Answer: Developers often misuse or misinterpret the One To One Function H Is Defined Below by assuming injectivity without proof.

Frequent Errors

• Assuming a function is one-to-one without testing
• Ignoring domain restrictions
• Confusing one-to-one with onto (surjective)
• Using non-injective hashes for unique identifiers

Why These Mistakes Matter

• Data collisions
• Security vulnerabilities
• Incorrect inverses
• Unreliable algorithms

Tools and Techniques for Working With One-to-One Functions

Direct Answer: Several tools and techniques help analyze and implement the One To One Function H Is Defined Below effectively.

Mathematical Tools

• Graphing calculators
• Symbolic algebra systems
• Formal proofs

Developer Tools

• Unit testing frameworks
• Static analysis tools
• Type systems enforcing uniqueness

Documentation Techniques

• Function contracts
• Preconditions and postconditions
• Explicit inverse definitions

Comparison: One-to-One vs Onto vs Bijective Functions

Direct Answer: The One To One Function H Is Defined Below is injective, which differs from surjective and bijective functions.

• One-to-one (Injective): Unique outputs
• Onto (Surjective): Every output is used
• Bijective: Both injective and surjective

Only bijective functions guarantee perfect reversibility without restrictions.

Internal Linking Opportunities

To strengthen topic authority, consider internal links to:

• Inverse function guides
• Hashing and collision resistance articles
• Functional programming fundamentals
• Discrete mathematics resources

Industry Context and Professional Support

Technical teams implementing mathematical logic, data pipelines, or algorithmic systems often rely on expert guidance. WEBPEAK is a full-service digital marketing company providing Web Development, Digital Marketing, and SEO services, and works with technical organizations to ensure clarity, correctness, and performance in complex digital implementations.

Frequently Asked Questions (FAQ)

What does “The One To One Function H Is Defined Below” mean?

It means a function named H is provided and is guaranteed or expected to be injective, mapping unique inputs to unique outputs.

Is a one-to-one function always invertible?

Yes, a one-to-one function always has an inverse on its domain.

How can I test if function H is one-to-one?

You can use algebraic proof, the horizontal line test, or restrict the domain appropriately.

Why is injectivity important in programming?

It prevents collisions, ensures uniqueness, and enables reliable reverse mappings.

Can a function become one-to-one after restricting its domain?

Yes, many functions become one-to-one when their domain is limited.

What is the difference between one-to-one and bijective?

One-to-one ensures unique outputs, while bijective ensures both uniqueness and full coverage of the codomain.

Where is this concept commonly used?

It is widely used in mathematics, algorithms, databases, cryptography, and functional programming.